Preface

This is a short post that covers advances in AI, and the current state of AI + possible future pathways. Here we cover two interesting talks in Reinforcement Learning, and Meta Learning.

Predictions on the Future of AI

Meta Learning

From the talk by Professor Ying Wei, at the City University of Hong Kong, there were new techniques highlighted that optimizes a Neural Scheduler through obtaining a temporal Meta Model. The Neural Scheduler, once optimized then updates the Meta Model. The technique by professor Wei is utilized as an Adaptive Task Scheduler (ATS), it is better than previous implementations of Task Scheduling, since it does not require a manual strategy design, and is better suited for Meta Learning Models. The ATS proposed by Professor Wei contains two Meta-model-related Factors¹. The steps are highlighted in the figures below.

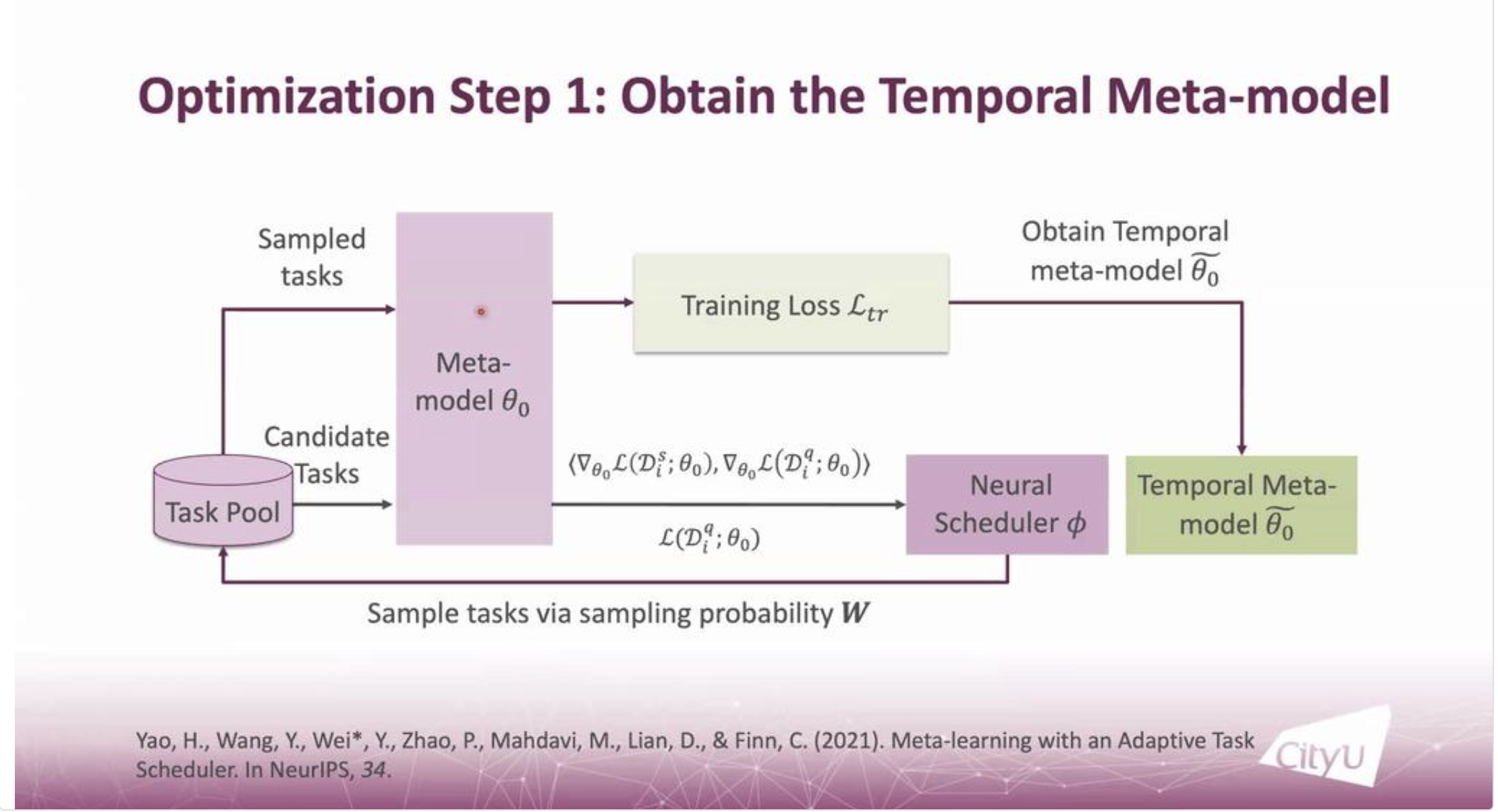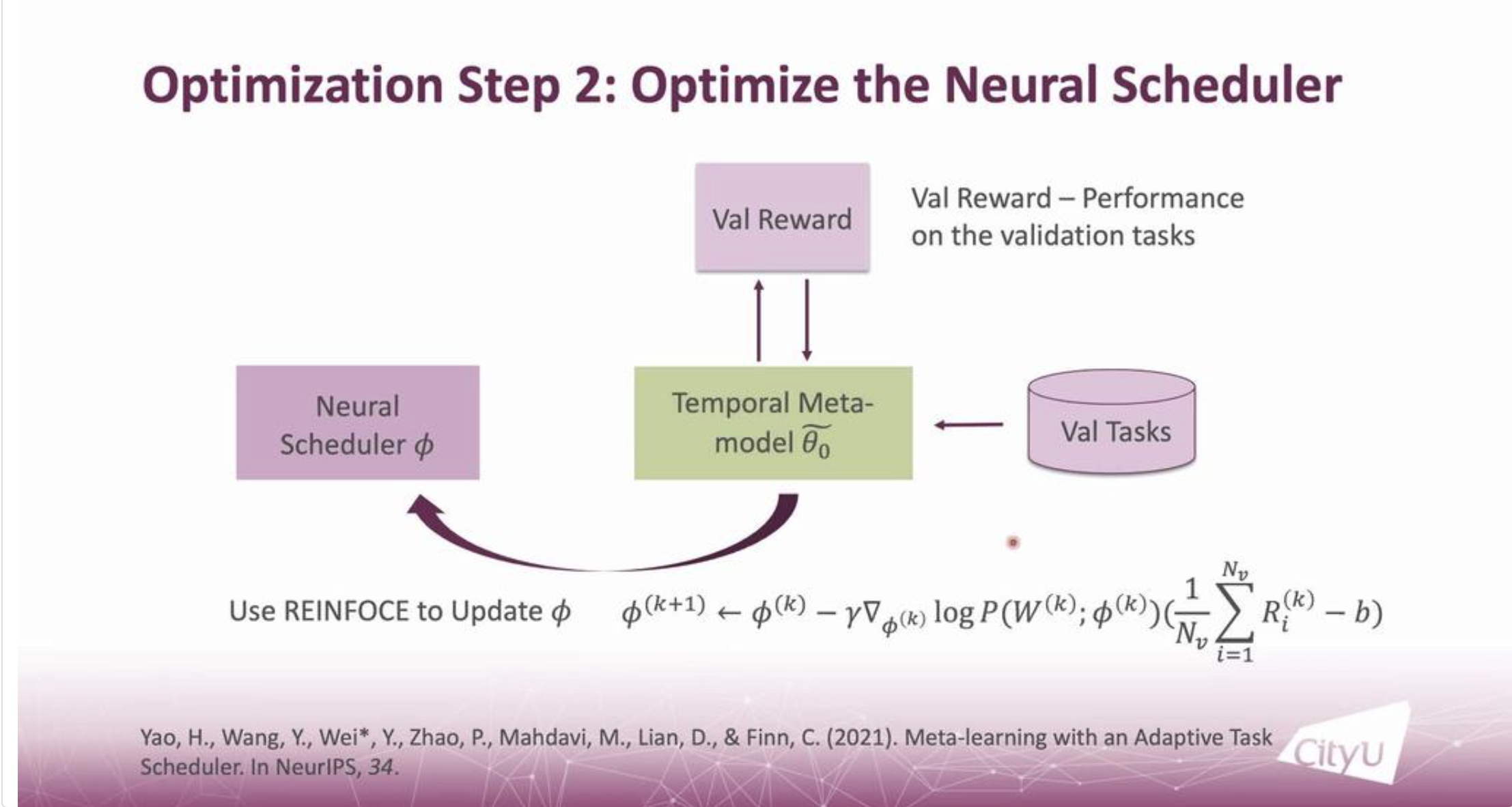This update strategy, while a noticeable improvement over previous Meta Learning accuracies is still far from satisfactory.

The key benefits of using ATS are:

1. It improves the “meta-training loss as long as the negative sampling probability is negatively correlated with losses and positively correlated with gradient similarities.”
2. ATS reacts differently depending on the models distance to the optimal solutions. • When the meta-model is far from the optimal solution, ATS speeds up training. • When the meta-model is within the variance of the optimal, ATS improves the generalization ability with more flat minima.
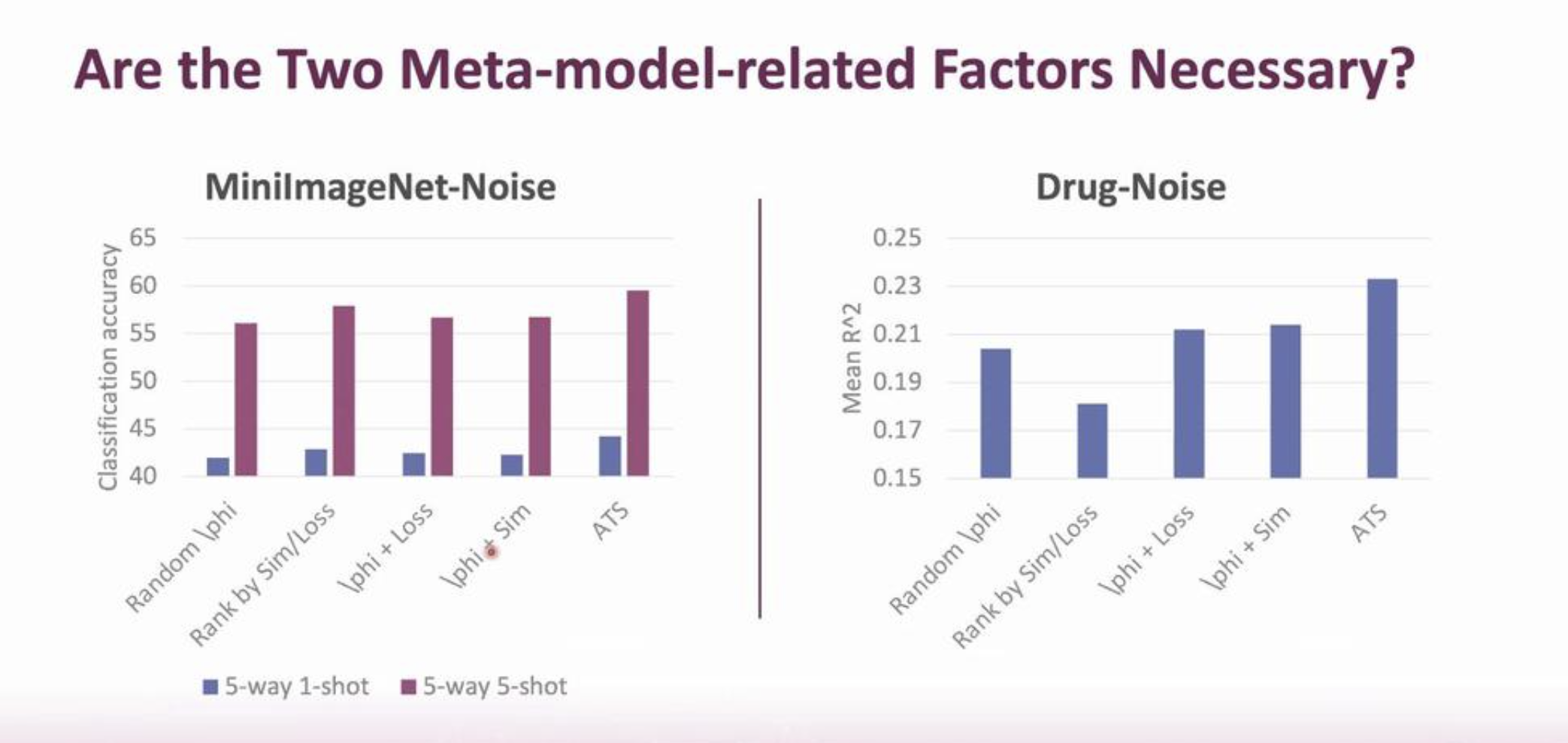
3. ATS consistently improves the generalization under noisy settings in different applications, better than 1) non-adaptive data schedulers, 2) non-adaptive task schedulers. See figure below.
4. As the noise ratio/scaler increases, ATS consisteltly outperfroms: 1) uniform sampling, 2) the bests non-adaptive sampling strategies, and shows even more significant improvements. The figure below shows the superior performance of ATS compared to the state-of-the art.

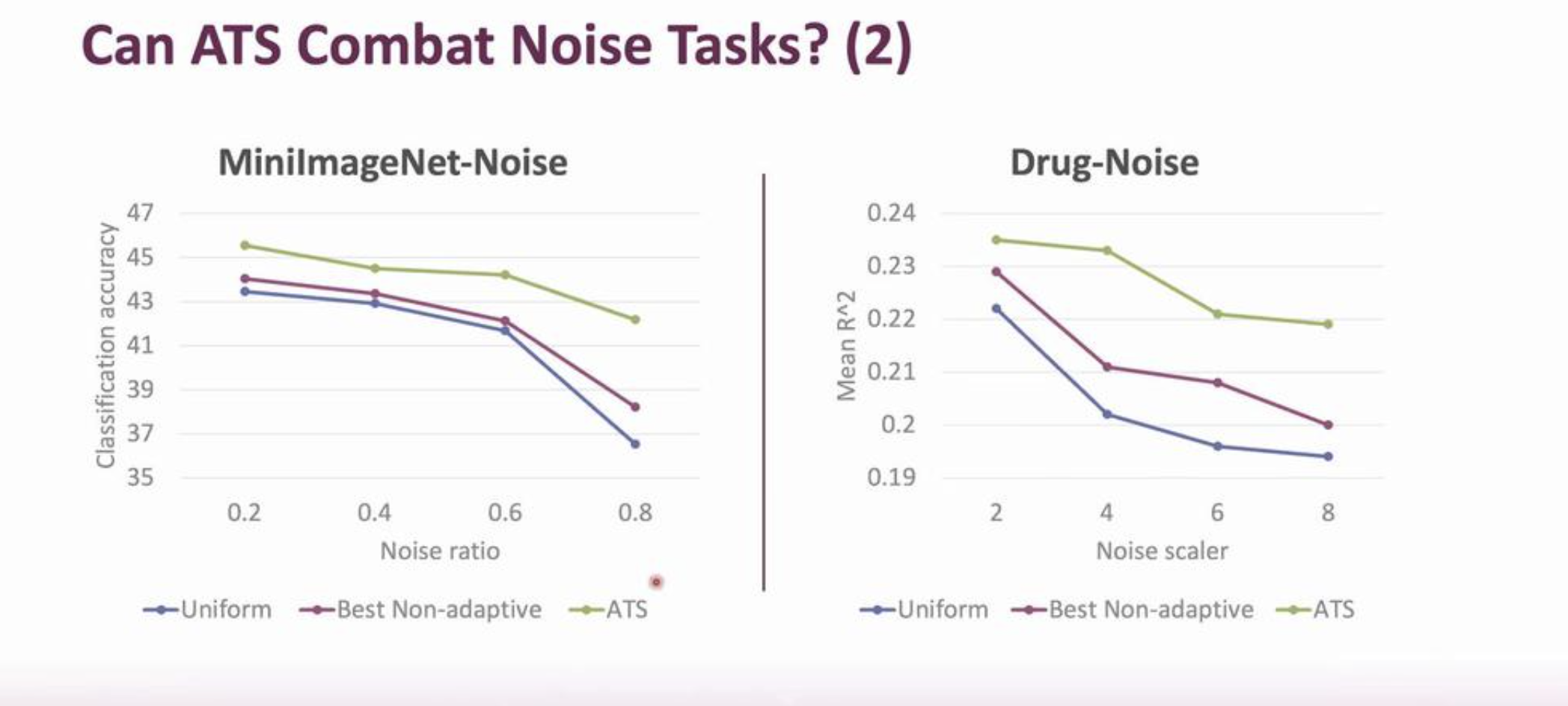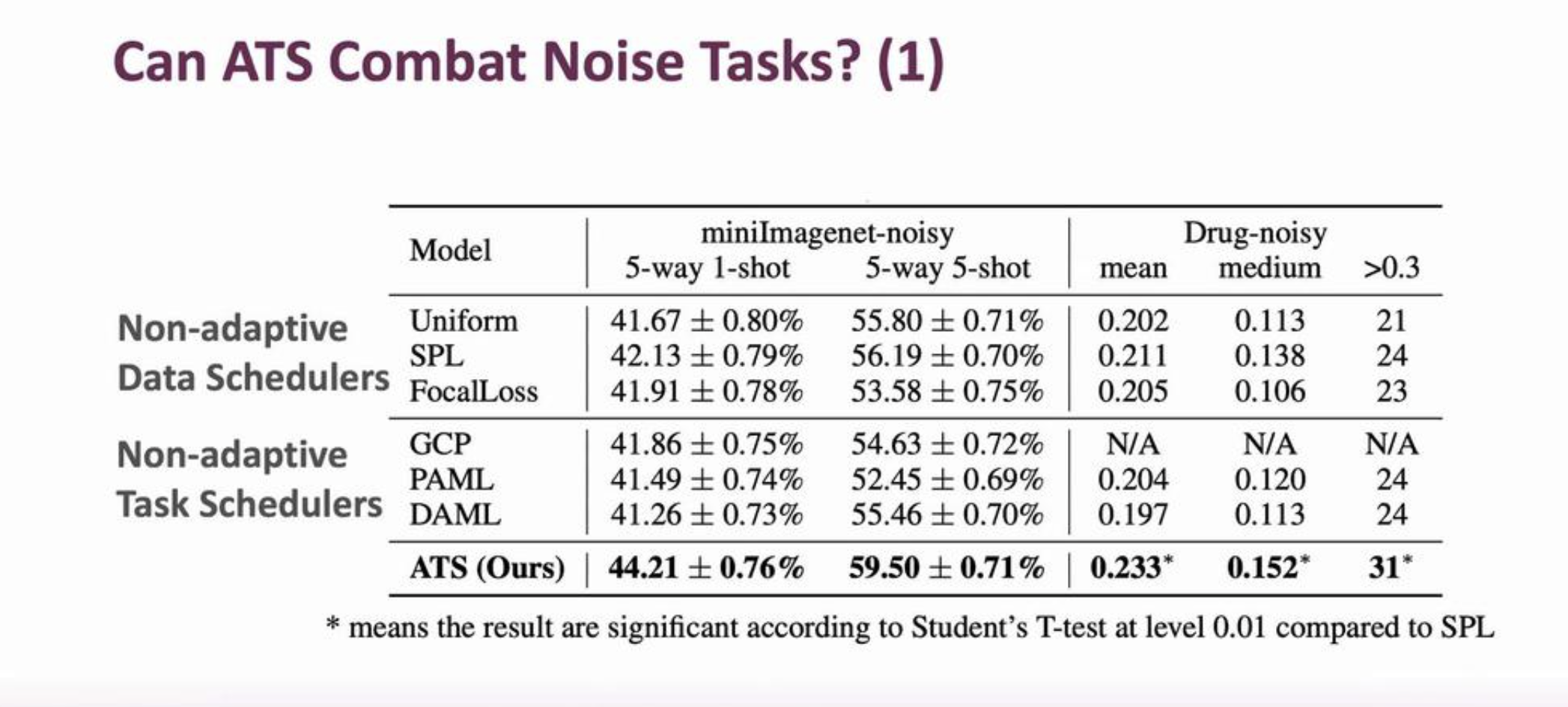Professor Wei also mentioned the importance of the neural scheduler in the pipeline, and the neccessity of two meta-model-related factors in the ATS.

Key Points

Professor Wei, in the figure below, summarizes the key improvements that meta learning needs to take on to be viable for real-world application.

All in all, meta-learning can be viable for future applications. It takes a few breakthroughs to push through the existing challenges and meet satisfactory performance benchmarks.

Reinforcement Learning

Reinforcement Learning (RL) is a field where, given a set of choices, an AI is set to make decisions based on rewards and tasks presented. The paper “On the Expressivity of Markov Reward”, was co-authored by researchers at Deepmind, Brown and Princeton². One of the Co-authors, Professor Doina Precup, is a Professor at McGill and I will be auditing her course: Reinforcement Learning in Winter 2022. I was planning on formally taking the course, but it was cancelled, and I am currently out of credits.

The paper jumps back to the basics of reinforcement learning, and studies the motivation of Reinforcement Learning. The paper focuses on: “Reward”. Reward is responsible for capturing goals, purposes, tasks and creating the correct learning dynamics to allow agents to achieve competence. Reward is introducted in RL, in the Sutton (2004), Littman (2017) reward hypothesis that states that any task can be achieved by an agent if given the right reward. The paper carries out a systematic analysis of the Suttom, Littman reward hypothesis.

It addresses the question: “For any choice of task, can Markov Reward always capture the chosen task?”

One of the main findings of the paper, which will be covered, is that not all tasks have corresponding rewards.

Markov Reward

The expression question: “Which signal can be used as a mechanism for expressing a task (to an agent)?” is answered by the reward hypothesis below: •Given any task T and any environment E there is a reward function that realizes T in E.
The reward hypothesis synthesizes that rewards can express tasks to agents. The validity of this hypothesis depends on what we mean by task, and we come to fundamentally challenge What defines a task.

The paper comes to think of a task as something reward is trying to capture, such as preferences. A few assumptions follow:

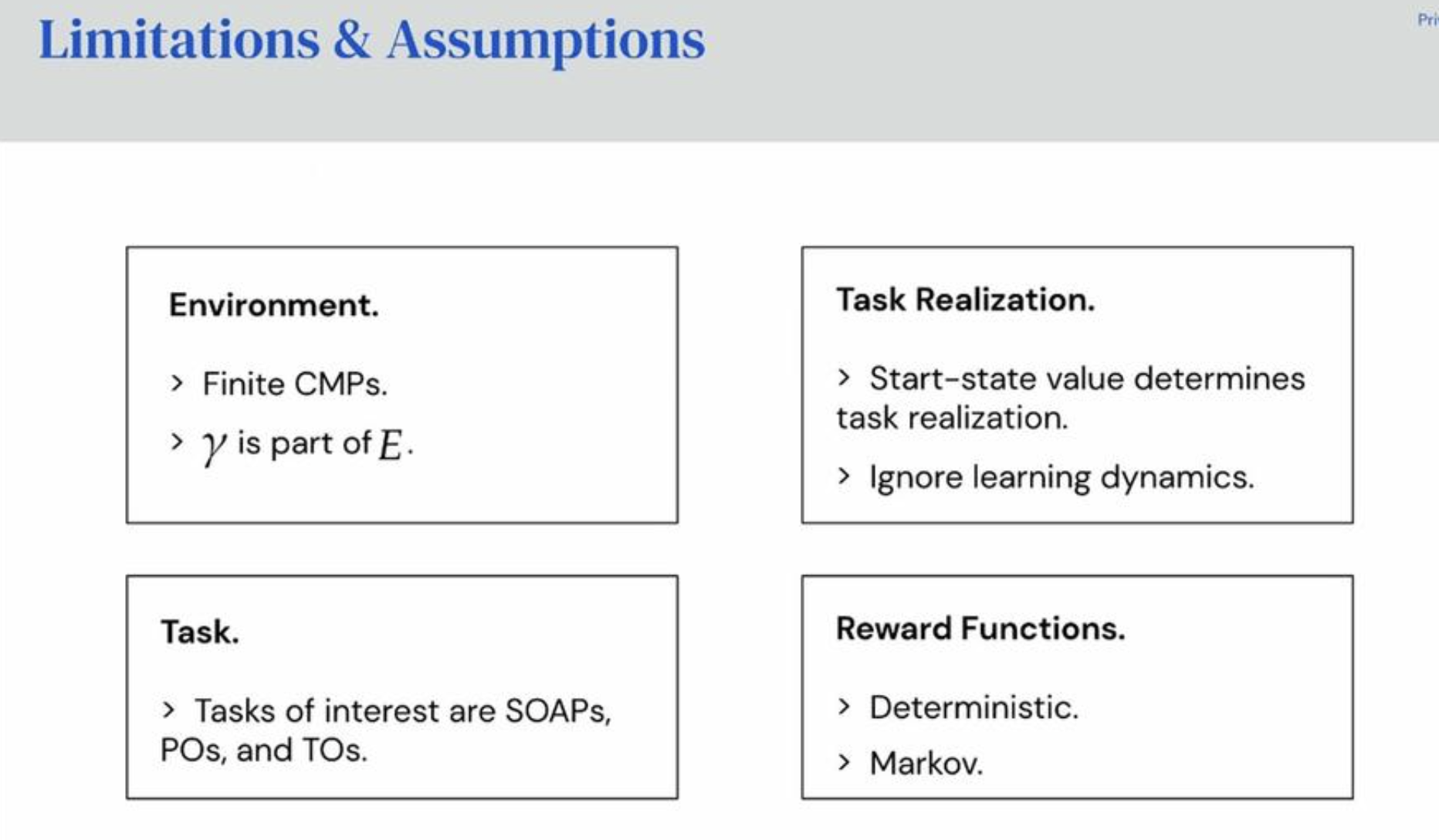
1. All environments are finite Controlled Markov Processes (CMPs).
2. Focus on Markov Reward Functions
3. Focus on Markov and the state of the given environment. • These can be a function of state, state action pairs, state action state triple.

The paper draws on the different definitions of reward from the literature (relevant references starred).

What is a Task?

The paper defines three types of tasks in Reinforcement Learning.

1. Set of Acceptable Policies (SOAP) • A set of good deterministic policies, that are better than the “bad” policies. • The union of the good and bad deterministic policies is the whole deterministic policy space.
2. Policy Ordering (PO) • A generalization of SOAP, where many tiers of policies exist.
3. Trajectory Ordering (TO) • Can articulate a set of goals that the policy should meet.

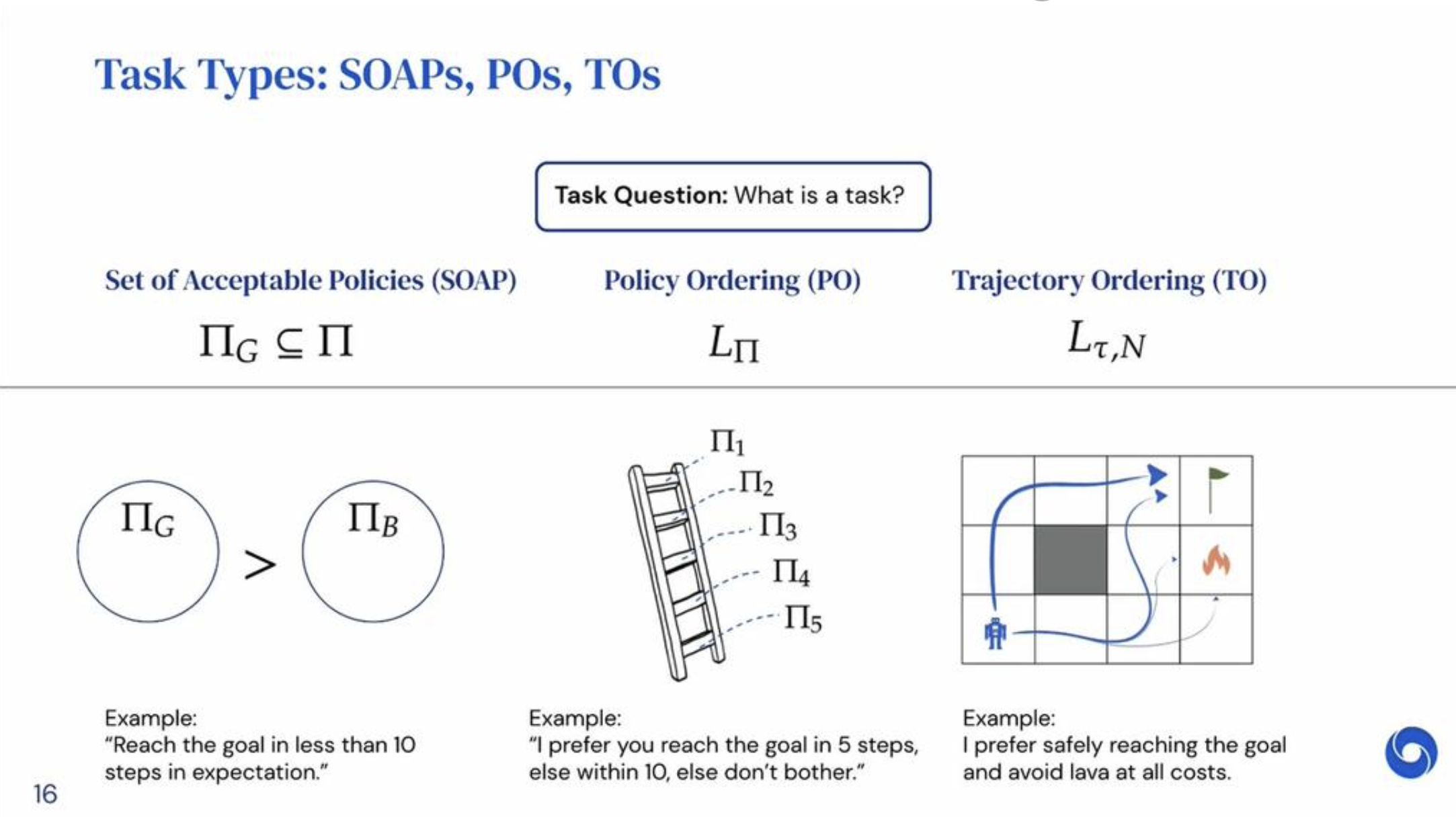
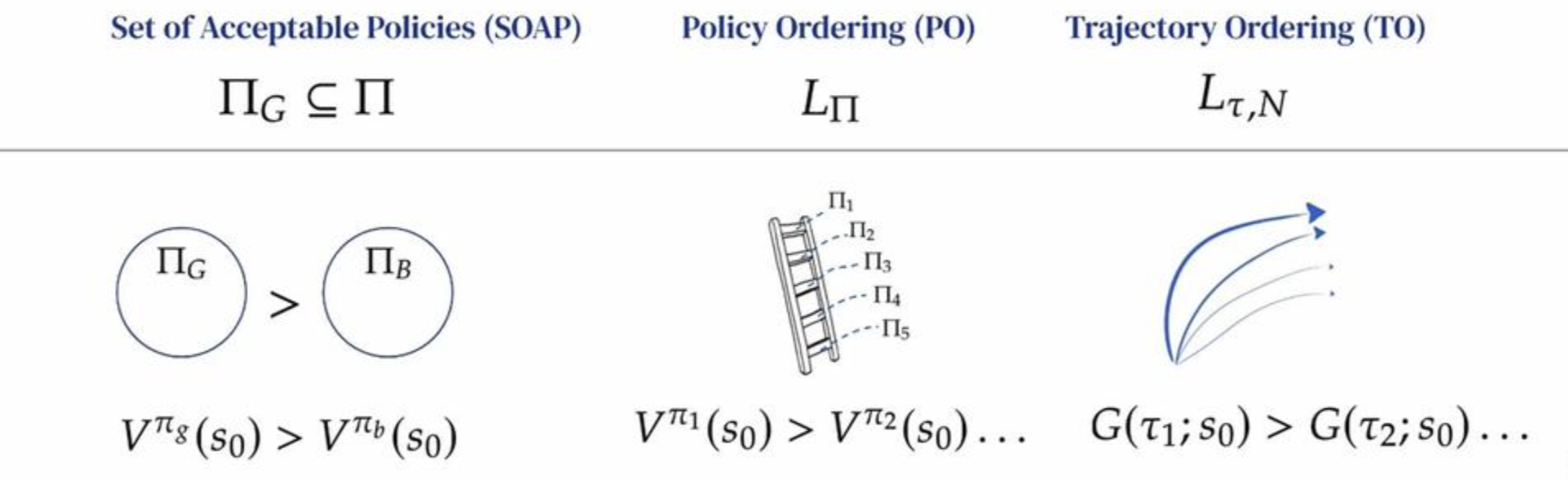
These types tasks seek to discriminate between secondary/non-optimal behaviours in their policies, since some secondary paths are better than others. If we revisit the reward hypothesis, the view of the paper is that, a reward function should realize a task throught its value function. In more simplified terms, if we use one of the three tasks defined above inside of an Environment E, a reward function of E should give us an Markov Decision Process (MDP). This in turn induces a Value Function for all policies. A task is realized when a value function agrees with its constraints.

So for each of our tasks:

1. SOAPs • Value functions should split policies between Good and Bad.
2. PO • Value function should order policies according to their tier
3. TO • Start-state return should order trajectories

Can Reward Always Express Tasks?

To answer the main question, we ask ourselves two sub-questions:

1. What Can Reward Express?

By answering sub-question 1, the paper reaches a conclusion: Theorem 1. For each SOAP, PO, and TO, there exist (E, T) pair for which no reward function realizes T in E. Note that to prove Theorem 1, all we need to do is find one counter example that disproves the opposite claim i.e. find an (E, T) pair for which no reward function realizes T in E.
One example that the paper gives is: Given an environment with a grid world, and X, Y coordinates as state. Our SOAP task is: “Always move in the same direction.”
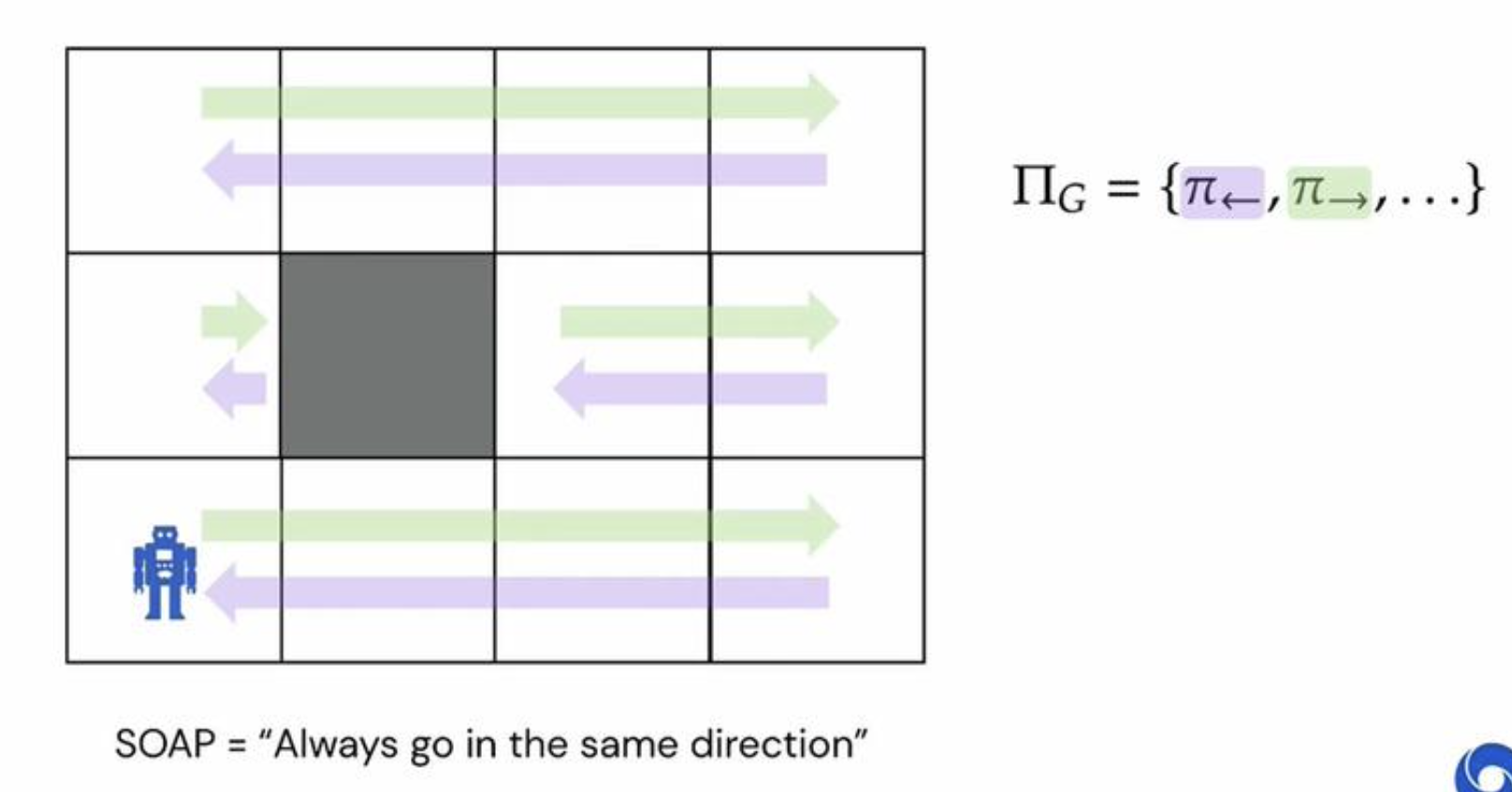
The issue with this task is that we can not find a singular policy that are strictly higher and start state value than all other policies. In simple terms, without knowledge of history, we don’t know if moving only left is better than moving only up, and this applies to all directions. A more indepth explanation can be found in the Paper.

2. Can We Find the Realizing Rewards?

Before we answer this question, it is important to know about the RewardDesignProblem. 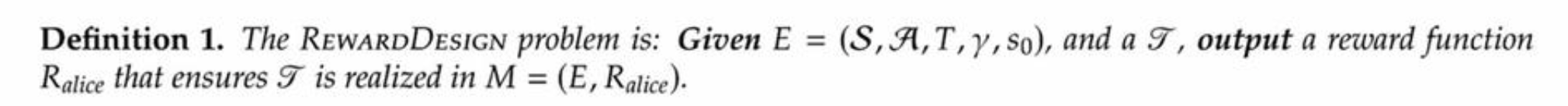This definition leads us to Theorem 2. The RewardDesignProblem can be solved in Polynomial time, for any finite E and any T. The realization from Theorem 2 allows us to “construct reward functions that exactly induce one of these tasks.”

Given Theorem 2, we construct a Corollary that allows us to determine when the reward function does not exist.
Corollary 1. Given T and E, deciding whether T is expressible in E is solvable in polynomial time for any finite E.
Given Corollary 1 if a task in a finite E does not have a reward function, then we will not be able to produce an output reward function in Polynomial time, hence it does not exist. -This reminds me of High School Geometry.

Limitations

Extra Information

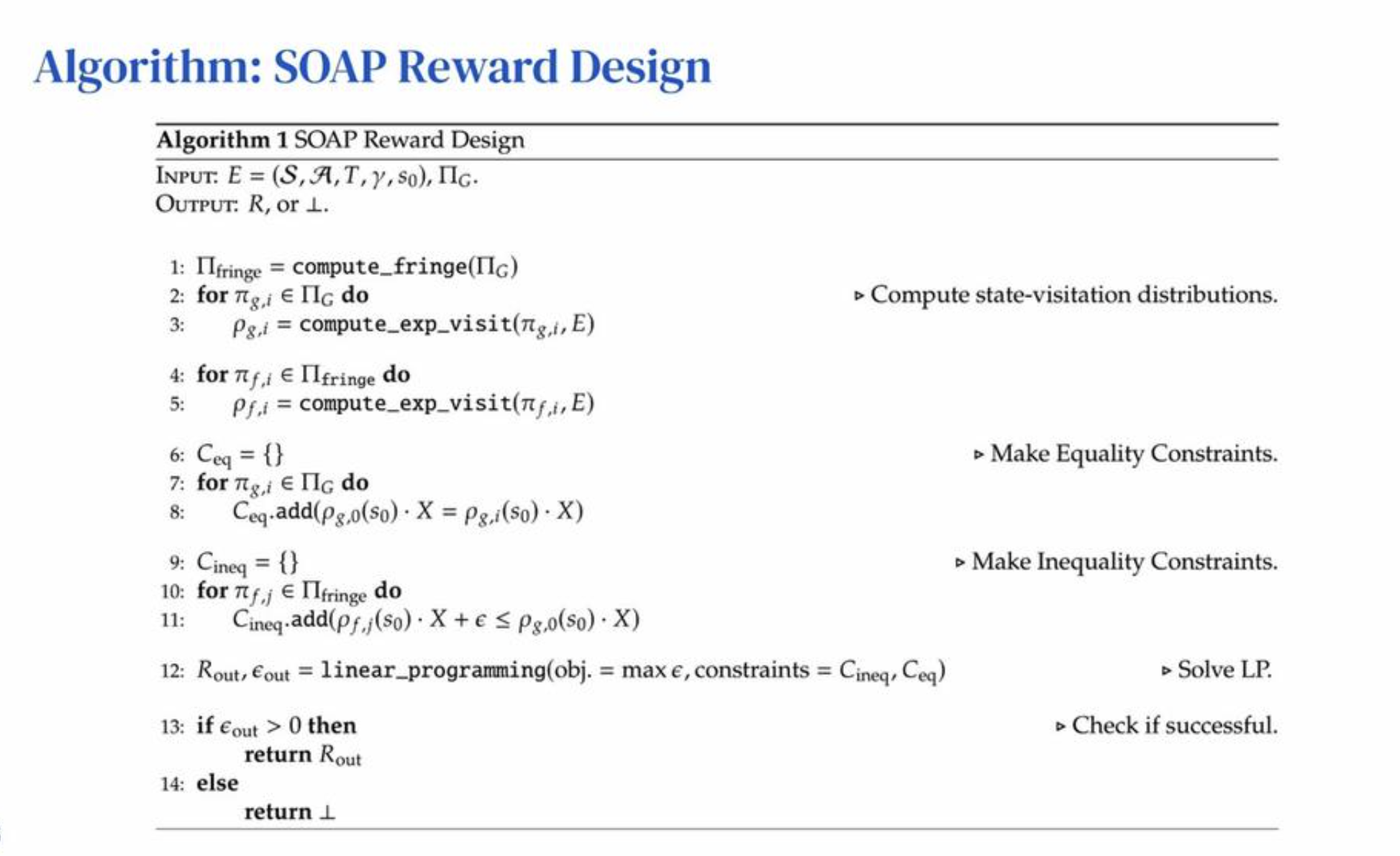For interesting and relevant Experiments related to Algorithms, and the three defined types of tasks please refer to the Paper.

Conclusion

Highlighting these two papers in Reinforcement Learning, and Meta-Learning show that in order to progress in AI there is still alot of room for improvement.

1. We learn from the Reinforcement Learning paper that we can progress by redefining the fundamental concepts, and then building upon them.
2. We learn from the Meta-Learning paper that, through tangential information, we can make jumps in our model accuracy. •The choice of using ATS was through researching relevant literature.

```